On a criterion  of  the finiteness  of the representation  type for families of the categories of injective representations

В. М. Бондаренко; М. В. Стьопочкіна

doi:10.24144/2616-7700.2022.41(2).16-22

Автор(и)

В. М. Бондаренко Інститут математики НАН України, Україна https://orcid.org/0000-0002-5064-9452
М. В. Стьопочкіна Поліський національний університет, Україна https://orcid.org/0000-0002-7270-9874

DOI:

https://doi.org/10.24144/2616-7700.2022.41(2).16-22

Ключові слова:

ін'єктивне зображення, критична ч. в. множина, квадратична форма Тітса для комутативних сагайдаків, скінченний зображквальний тип, додатність та слабка додатність

Анотація

Зображення ч. в. множин (частково впорядкованих множин), введені Л. А. Назаровою і А. В. Ройтером у 1972 р., відіграють важливу роль у сучасній теорії зображень та її застосуваннях. М. М. Клейнер отримав опис ч. в. множин скінченного зображувального типу в термінах критичних ч. в . множин (мінімальних ч. в. множин нескінченного зображувального типу), а Ю. А. Дрозд довів, що ч. в. множина S (яка не містить елемента, позначеного як 0) має скінченний зображувальний тип тоді і тільки тоді, коли її квадратична форма Тітса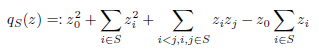

є слабко додатною, тобто додатною на множині невід’ємних векторів (у 1972 та 1974 роках відповідно). У цій статті ми розглядаємо ситуацію (що стосується нескінченних ч. в. множин), коли головну роль відіграє не слабка додатність, а додатність квадратичної форми Тітса. Ситуація стосується дослідження категорій зображень спеціального вигляду, і в цьому випадку ми використовуємо встановлений першим автором зв'язок між квадратичними формами Тітса для частково впорядкованих множин і комутативних сагайдаків.

Посилання

Nazarova, L. A., & Roiter, A. V. (1972). Representations of partially ordered sets. Zap. Nauchn. Sem. LOMI, 28, 5‒31 [in Russian].

Kleiner, M. M. (1972). Partially ordered sets of finite type. Zap. Nauchn. Sem. LOMI, 28, 32‒41 [in Russian].

Drozd, Yu. A. (1974). Coxeter transformations and representations of partially ordered sets. Funkts. Anal. Prilozh., 8(3), 34‒42 [in Russian].

Nazarova, L. A. (1975). Partially ordered sets of infinite type. Izv. Akad. Nauk SSSR Ser. Mat., 39(5), 963‒991 [in Russian].

Plakhotnik, V. V. (1976). Representations of partially ordered sets over commutative rings. Izv. Akad. Nauk SSSR Ser. Mat., 40(3), 527‒543 [in Russian].

Bondarenko, V. M., Zavadskij, A. G., & Nazarova, L. A. (1979). On representations of tame partially ordered sets. Representations and Quadratic Forms. Inst. Math. Acad. Sci. Ukrain. SSR, 75‒105 [in Russian].

Bondarenko, V. M. (1988). Bundles of semi-chains and their representations. Inst. Math. Acad. Sci. Ukrain. SSR, Preprint 88.50 [in Russian].

Nazarova, L. A., Bondarenko, V. M., & Roiter, A. V. (1991). Tame partially ordered sets with involution. Proc. Steklov Inst. Math., 183, 149‒159 [in Russian].

Bondarenko, V. M., & Zavadskij, A. G. (1991). Posets with an equivalence relation of tame type and of finite growth. CSM Conf. Proc. 11, 67‒88.

Zavadskij, A. G. (1991). Differentiation algorithm and classification of representations. Izv. Akad. Nauk SSSR Ser. Mat., 55(5), 1007‒1048 [in Russian].

Belousov, K. I., Nazarova, L. A., & Roiter, A. V. (1997). Finitely representable triadic sets. Algebra Anal., 9(4), 3‒27 [in Russian].

Belousov, K. I., Nazarova, L. A., & Roiter, A. V. (1997). Finitely represented dyadic sets and their multielementary representations. Ukr. Mat. Zh., 49(11), 1465‒1477 [in Russian].

Bondarenko, V. M. (2003) Linear operators on S-graded vector spaces. Linear Algebra Appl., 365, 45‒90.

Zavadskij, A. G. (2003). Tame equipped posets. Linear Algebra Appl., 365, 389‒465.

Bondarenko, V. M., & Styopochkina, M. V. (2005). (Min, max)-equivalence of partially ordered sets and the Tits quadratic form. Problems of Analysis and Algebra: Zb. Pr. Inst. Mat. NAN Ukr., 2(3), 18‒58 [in Russian].

Bondarenko, V. M. (2005). On (min, max)-equivalence of posets and applications to the Tits forms. Bull. of Taras Shevchenko University of Kyiv. (series: Physics & Mathematics), 1, 24‒25.

Bondarenko, V. M., & Styopochkina, M. V. (2005). Partially ordered sets of injective type. Scien. Bull. of Uzhhorod Univ. Series of Math. and Inform., 10‒11, 22‒33 [in Russian].

Bondarenko, V. M., & Styopochkina, M. V. (2006). On finite posets of inj-finite type and their Tits forms. Algebra Discret. Math., (2), 17‒21.

Brenner, S. (1974). Quivers with commutativity conditions and some phenomenology of forms. Proc. of Intern. Conference of Representations of Algebras. Carleton Univ., Ottawa, Ontariю

Gabriel, P. (1972). Unzerlegbare Darstellungen. Manuscripta Math., 6, 71‒103.

Brenner, S., & Butler, M. C. R. (1979). Generalizations of the Bernstein-Gelfand-Ponomarev reflection functors. Representation theory, II (Proc. Second Intern. Conference, Carleton Univ., Ottawa, Ont.), 103‒169.

Bongartz, K. (1983). Algebras and quadratic forms. J. London Math. Soc. 2, 28(3), 461‒469.

Zavadskij, A. G., & Shkabara, A. C. (1976). Commutative quivers and matrix algebras of finite type. Inst. Math. Acad. Sci. Ukrain. SSR, Preprint 76.03, 52 p. [in Russian].

Bondarenko, V. M. (2006). On a connection between Drozd and Brenner quadratic forms (the case of unbounded posets). Ukr. Mat. Visn., 3(2), 153‒165 [in Russian].