Classification of the posets of MM-type being the symmetric oversupercritical poset of order 9

В. М. Бондаренко; М. В. Стьопочкіна

doi:10.24144/2616-7700.2024.44(1).7-14

Автор(и)

В. М. Бондаренко Інститут математики НАН України, Україна https://orcid.org/0000-0002-5064-9452
М. В. Стьопочкіна Поліський національний університет, Україна https://orcid.org/0000-0002-7270-9874

DOI:

https://doi.org/10.24144/2616-7700.2024.44(1).7-14

Ключові слова:

зображення, критична та суперкритична ч. в. множина, надсуперкритична ч. в. множина, квадратична форма Тітса, скінченний і ручний зображувальний тип, додатність і слабка додатність, негативність і слабка негативність

Анотація

Зображення ч. в. множин (частково впорядкованих множин) над полем ввели Л. А. Назарова i А. В. Ройтер в 1972 р., i перший автор був одним iз тих, хто брав активну участь у розвитку вiдповiдної теорiї. Першим критерiєм у нiй був отриманий М. М. Клейнером критерiй скiнченностi зображувального типу. У 1992 р. вiн довiв, що ч. в. множина S має скiнченний зображувальний тип тодi i лише тодi, коли во-ни не мiстить повних ч. в. пiдмножин вигляду K₁ = (1, 1, 1, 1), K₂ = (2, 2, 2), K₃ = (1, 3, 3), K₄ = (1, 2, 5) і K₅ = (N, 4). Цi ч. в. множин називаються критичними ч. в. множинами (щодо скiнченностi типу) в тому сенсi, що це мiнiмальнi ч. в. множин з нескiнченною кiлькiстю нерозкладних зображень, з точнiстю до еквiвалентностi). Тепер їх також називають ч. в. множинами Клейнера. У 1974 р. Ю. А. Дрозд довiв, що ч. в. множина S має скiнченний зображувальний тип тодi i лише тодi, коли її квадратична форма Тiтса

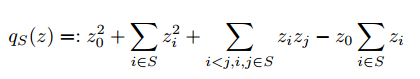
є слабко додатною (тобто додатною на множинi невiд’ємних векторiв). Отже, ч. в. множини Клейнера є також критичними щодо слабкої додатностi квадратичної фор-ми Тiтса. У 2005 р. автори довели що ч. в. множин є критичною щодо додатностi квадратичної форми Тiтса тодi i лише тодi, коли вона є мiнiмаксно iзоморфна деякiй ч. в. множинi Клейнера.

Подiбну ситуацiю маємо з ч. в. множинами ручного зображувального типу. У 1975 р. Л. А. Назарова довела, що ч. в. множина S є ручною тодi i лише тодi, коли вона не мiстить ч. в. пiдмножин вигляду N₁ = (1, 1, 1, 1, 1), N₂ = (1, 1, 1, 2), N₃ = (2, 2, 3), N₄ = (1, 3, 4), N₅ = (1, 2, 6) і (N, 5). Отже, цi ч. в. множини є критичними щодо ручного зображувального типу i вона назвала їх суперкритичними; вони є також критичними щодо слабкої невiд’ємностi квадратичної форми Тiтса. У 2009 роцi автори довели, що ч. в. множина є критичною щодо невiд’ємностi квадратичної форми Тiтса тодi i лише тодi, коли вона мiнiмаксно iзоморфна деякiй суперкритичнiй ч. в. множинi.

Перший автор запропонував ввести ч. в. множини (названi надсуперкритичними), якi вiдрiзняються вiд суперкритичних ч. в. множин в тiй же мiрi, що суперкритичнi вiдрiзняються вiд критичних.

У попереднiх статтях автори описали (з точнiстю до iзоморфiзму) всi ч. в. множини, мiнiмаксно iзоморфнi довiльнiй надсуперкритичнiй множинi, окрiм (1,4,4), i вивчили деякi їхнi комбiнаторнi властивостi. У цiй статтi розглядається випадок ч. в. множини (1, 4, 4).

Посилання

Nazarova, L. A., & Roiter, A. V. (1972). Representations of partially ordered sets. Zap. Nauchn. Sem. LOMI, 28, 5–31 [in Russian].

Kleiner, M. M. (1972). Partially ordered sets of finite type. Zap. Nauchn. Sem. LOMI, 28, 32–41 [in Russian].

Drozd, Yu. A. (1974). Coxeter transformations and representations of partially ordered sets. Funkts. Anal. Prilozh., 8(3), 34–42 [in Russian].

Nazarova, L. A. (1975). Partially ordered sets of infinite type. Izv. Akad. Nauk SSSR Ser. Mat., 39(5), 963–991 [in Russian].

Bondarenko, V. M., Zavadskij, A. G., & Nazarova, L. A. (1979). On representations of tame partially ordered sets. Representations and Quadratic Forms. Inst. Math. Acad. Sci. Ukrain. SSR, 75–105 [in Russian].

Bondarenko, V. M. (1983). Exact partially ordered sets of infinite growth. Linear Algebra and Representation Theory. Inst. Math. Acad. Sci. Ukrain. SSR, 68–85 [in Russian].

Bondarenko, V. M., Nazarova, L. A„ & Roiter, A. V. (1986). Representations of partially ordered sets with involution. Inst. Math. Acad. Sci. Ukrain. SSR, Preprint 86.80, 24p. [in Russian].

Bondarenko, V. M. (1988). Bundles of semi-chains and their representations. Inst. Math. Acad. Sci. Ukrain. SSR, Preprint 88.50, 32 p. [in Russian].

Nazarova, L. A., Bondarenko, V. M., & Roiter, A. V. (1991) Tame partially ordered sets with involution. Proc. Steklov Inst. Math., 183, 149–159 [in Russian].

Bondarenko, V. M., & Zavadskij, A. G. (1991) Posets with an equivalence relation of tame type and of finite growth. CSM Conf. Proc., 11, 67–88.

Zavadskij, A. G. (1991) Differentiation algorithm and classification of representations. Izv. Akad. Nauk SSSR Ser. Mat., 55(5), 1007–1048 [in Russian].

Bondarenko, V. M., & Styopochkina, M. V. (2005). (Min, max)-equivalence of partially ordered sets and the Tits quadratic form. Problems of Analysis and Algebra: Zb. Pr. Inst. Mat. NAN Ukr., 2(3), 18–58 [in Russian].

Bondarenko, V. M. (2005). On (min, max)-equivalence of posets and applications to the Tits forms. Bull. of Taras Shevchenko University of Kyiv. (series: Physics & Mathematics), (1), 24–25.

Bondarenko, V. M., & Styopochkina, M. V. (2008). (Min, max)-equivalence of posets and nonnegative Tits forms. Ukr. Math. J., 60(9), 1349–1359.

Bondarenko, V. M., & Styopochkina, M. V. (2009). Description of posets critical with respect to the nonnegativity of the quadratic Tits form. Ukr. Math. J., 61(5), 734–746.

Bondarenko, V. V., Bondarenko, V. M., Styopochkina, M. V., & Chervyakov, I. V. (2011). 1-oversupercritical partially ordered sets with trivial group of automorphisms and minequivalence. Scien. Bull. of Uzhhorod Univ. Series of Math. and Inform., 22(2), 17–25 [in Russian].

Bondarenko, V. V., & Styopochkina, M. V. (2013). Non-primitive 1-oversupercritical partially ordered set and min-equivalence. Scien. J. of NPU named after Dragomanov. Series 1. Phys.-Math. sciences, 14, 55–61 [in Russian].

Bondarenko, V. M., & Styopochkina, M. V. (2021). On posets of sixth order having over-supercritical MM-type. Scien. Bull. of Uzhhorod Univ. Series of Math. and Inform., 38(1), 7–15.

Bondarenko, V. M., & Styopochkina, M. V. (2023). Classification of the posets of minmax type which are symmetric oversupercritical posets of the eighth order. Math. methods and phys.-mech. fields, 66(1-2), 1–11.

Bondarenko, V. M., & Styopochkina, M. V. (2018). On properties of posets of MM-type (1,3,5). Scien. Bull. of Uzhhorod Univ. Series of Math. and Inform., 32(1), 50–53.

Bondarenko, V. M., & Styopochkina, M. V. (2023). Classification of the posets of minmax type which are symmetric oversupercritical posets of the eighth order. Math. Sci. (N.Y.), 274(5), 583–593.