Класифікація неізоморфних груп деякого класу черніковських 3-груп
DOI:
https://doi.org/10.24144/2616-7700.2024.44(1).37-45Ключові слова:
черніковська група, матричне зображення групи, незвідна компонента зображенняАнотація
В цiй роботi описуються з точнiстю до iзоморфiзму деякi чернiкоськi 3-групи, що є циклiчними розширеннями повних абелевих 3-груп з умовою мiнiмальностi.
Нехай ℂ3∞ — адитивна квазiциклiчна 3-група, а ℂn3∞ — зовнiшня пряма сума n екземплярiв квазiциклiчної 3-групи ℂ3∞ для деякого натурального числа n. Добре вiдомо, що група Aut ℂn3∞ iзоморфна повнiй лiнiйнiй групi GL(n, ℤ3), де ℤ3 — кiльце цiлих 3-адичних чисел. Тому надалi для довiльної матрицi A ∈ GL(n, ℤ3) та довiльного елемента c ∈ ℂn3∞ через A(c) позначатимемо образ елемента c при автоморфiзмi, що вiдповiдає матрицi A. Нехай {ar | r ∈ ℕ0} — множина всiх твiрних елементiв групи ℂn3∞, де ℕ0 = ℕ ∪ {0}, причому 3a0 = 0, 3ar = ar-1 для довiльного r ∈ ℕ.
Розглянемо циклiчну адитивну групу H порядку 27 з твiрним елементом h i деяке матричне зображення Γ цiєї групи степеня n над кiльцем ℤ3. Образ будь-якого елемента h' групи H позначатимемо через Γh'. Визначимо дiю · групи H на групi ℂn3∞ за правилом h' · c = Γh' (c) для довiльних елементiв h' ∈ H i c ∈ ℂn3∞. Пiдкре-слимо, що ядро Ker Γ є пiдгрупою стабiлiзатора кожного елемента iз ℂn3∞. Нескладно переконатися, що множина
A(ℂn3∞, H, Γ) = {c ∈ ℂn3∞ | h · c = c}
є пiдгрупою групи ℂn3∞. Для матричного зображення Γ групи H та деякого елемента c ∈ A(ℂn3∞, H, Γ) побудуємо групу G(Γ, c) наступним чином:
G(Γ, c) = H × ℂn3∞,
а бiнарна операцiя + задається так
(ih, c1) + (jh, c2) = ((i + j)h, μi,j + jh · c1 + c2),
де i, j ∈ {0, 1, . . . , 26}, c1, c2 ∈ ℂn3∞,
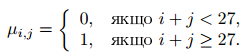
Вiдомо, що таким чином побудована група є циклiчним розширенням групи ℂn3∞ за допомогою групи H, а як наслiдок, є чернiковською 3-групою.
В роботi описанi з точнiстю до iзоморфiзму всi чернiковськi 3-групи, фактор-група яких за максимальною повною абелевою пiдгрупою є циклiчною групою порядку 27 i якi визначаються матричним ℤ3-зображенням [3]
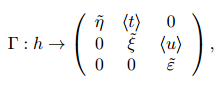
де ῆ — незвiдна ℤ3-матриця 18-го порядку вигляду
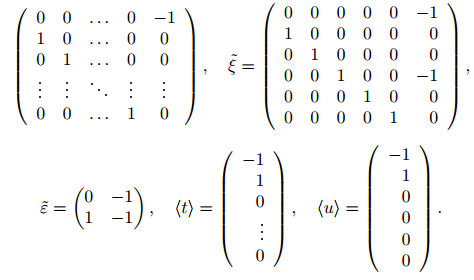
Посилання
- Gudivok, P. M., Vashchuk, F. G., & Drobotenko, V. S. (1992). Chernikov p-groups and integer p-adic representations of finite groups. Ukr. Mat. J., 44(6), 742–753.
- Gudivok, P. M., & Shapochka, I. V. (1999). On the Chernikov p-groups. Ukr. Mat. J., 51(3), 291–304.
- Gudivok, P. M., & Rud’ko, V. P. (1966). On p-adic integral representations of the cyclic p-group. Dopovidi Akad. Nauk URSR, 9, 1111–1113.
##submission.downloads##
Опубліковано
Як цитувати
Номер
Розділ
Ліцензія
Авторське право (c) 2024 І. М. Порохнавець, І. В. Шапочка

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.
Автори залишають за собою право на авторство своєї роботи та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons Attribution License, котра дозволяє іншим особам вільно розповсюджувати опубліковану роботу з обов'язковим посиланням на авторів оригінальної роботи та першу публікацію роботи у цьому журналі.








