On minimal minimax systems of generators for positive posets

В. М. Бондаренко; М. В. Стьопочкіна

doi:10.24144/2616-7700.2024.45(2).46-55

Автор(и)

В. М. Бондаренко Інститут математики НАН України, Україна https://orcid.org/0000-0002-5064-9452
М. В. Стьопочкіна Поліський національний університет, Україна https://orcid.org/0000-0002-7270-9874

DOI:

https://doi.org/10.24144/2616-7700.2024.45(2).46-55

Ключові слова:

додатна квадратична форма, квадратична форма Тiтса, додатна ч. в. множина, мiнiмаксна еквiвалентнiсть та iзоморфiзм, мінімаксна система твірних

Анотація

Зображення частково впорядкованих множин (скорочено ч. в. множин), введених Л. А. Назаровою i А. В. Ройтером (у матричнiй формi) в 1972 р., вiдiграють важливу роль у сучаснiй теорiї зображень та її застосуваннях. Ю. А. Дрозд у 1974 р. довiв, що ч. в. множина S має скiнченний зображувальний тип над полем тодi i лише тодi, коли її квадратична форма Тiтса

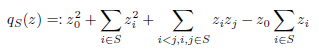
$eq.png$

є слабко додатною (тобто додатною на множинi невiд’ємних векторiв), але це твердження не є правильним, на вiдмiну вiд випадку сагайдакiв, коли розглядаються додатнi форми. Тому ч. в. множини з додатною квадратичною формою Тiтса викликали великий iнтерес з рiзних точок зору як аналоги дiаграм Динкiна. У 2005 р. автори описали з точнiстю до iзоморфiзму всi множини з додатною квадратичною формою Тiтса. Основним методом вирiшення цiєї проблеми є так званий метод мiнiмаксної еквiвалентностi, запропонований першим автором. Нещодавно вiн представив деяке поняття (а саме, мiнiмаксної системи твiрних) з розглядом вiдповiдних прикладiв, якi можна розглянути як появу нової теорiї, яка дослiджує комбiнаторнi властивостi множин вiдносно мiнiмаксної еквiвалентностi.

У цiй статтi ми вивчаємо з такої нової точки зору ч. в. множини з додатною ква-дратичною формою Тiтса (якi називаються додатними).

Біографії авторів

В. М. Бондаренко, Інститут математики НАН України

Провідний науковий співробітник відділу алгебри та топології. Доктор фізико-математичних наук

М. В. Стьопочкіна, Поліський національний університет

Доцент кафедри вищої та прикладної математики. Кандидат фізико-математичних наук

Посилання

Gabriel, P. (1972). Unzerlegbare Darstellungen I. Manuscripts Math., 6, 71–103. https://doi.org/10.1007/BF01298413
Drozd, Yu. A. (1974). Coxeter transformations and representations of partially ordered sets. Funkts. Anal. Prilozh., 8(3), 219–225. https://doi.org/10.1007/BF01075695 [in Russian].
Nazarova, L. A., & Roiter, A. V. (1972). Representations of partially ordered sets. Zap. Nauchn. Sem. LOMI, 28, 5–31. [in Russian].
Bondarenko, V. M., & Styopochkina, M. V. (2005). On posets of width two with positive Tits form. Algebra and Discr. Math., 12(2), 585–606.
Bondarenko, V. M., & Styopochkina, M. V. (2005). (Min, max)-equivalence of partially ordered sets and the Tits quadratic form. Problems of Analysis and Algebra: Zb. Pr. Inst. Mat. NAN Ukr., 2(3), 18–58 [in Russian].
Bondarenko, V. M. (2005). On (min, max)-equivalence of posets and applications to the Tits forms. Bull. of Taras Shevchenko University of Kyiv. (series: Physics & Mathematics), (1), 24–25.
Bondarenko, V. M. (2024). Minimax equivalence method: initial ideas, first applications and new concepts. Algebra and Discr. Math., 38(1), 1–22. https://doi.org/10.12958/adm2332
Kleiner, M. M. (1972). Partially ordered sets of finite type. Zap. Nauchn. Sem. LOMI, 28, 32–41. [in Russian].